'합차공식'에 해당 되는 글 1건
- 2010.02.03 삼각함수의 합차공식에 대한 증명 2
고등학교 3학년이 되어 심화 미적분을 배우면 삼각함수와 관련된 여러 공식들을 배우게 된다. 이들에 대한 자세한 유도는 책에 있지만 벡터의 내적을 이용한 증명이 가장 단순하고 기억하기 쉬운 것 같다.
코사인이나 사인에 관한 합차공식 중 아무거나 하나만 증명하면 나머지 공식들은 이로부터 우글우글 쏟아져 나오므로 맨 처음 시작만을 적겠다.
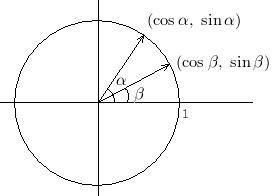
위와 같이 길이가 1인 두 벡터를 생각하자. 이제 두 벡터의 내적을 구하면
\(|1||1|\cos(\alpha - \beta) = \cos\alpha \cos\beta + \sin\alpha \sin\beta\)
이다. \(\beta\) 대신에 \(-\beta\)를 대입하면 \(\cos(\alpha+\beta)\)에 대한 공식을 구할 수 있다. 다시 \(\beta\) 대신에 \(\beta-\pi/2\)를 대입하면 \(\sin(\alpha + \beta)\)에 대한 공식을 얻을 수 있다 (\(\cos(\theta-\pi/2) = \sin\theta\)이므로...). 이런 식으로 다른 공식들을 하나씩 증명해 나갈 수 있다.
 Prev
Prev