'공부이야기/수학 이야기'에 해당 되는 글 14건
- 2013.11.11 점과 직선 사이의 거리 공식: 벡터의 내적을 이용한 유도 5
- 2013.11.06 평면 위의 점과 직선 사이의 거리 공식: 미분을 이용한 유도 3
- 2013.08.23 수학 글쓰기 - 계승혁
- 2013.03.14 The Grammar According to West by Douglas B. West
- 2011.07.18 Hitler Learns Topology
- 2010.07.19 새로 바뀐 고등학교 수학 과목들(수갤 magicclaus님 글 펌)
- 2010.07.06 이항분포의 평균과 분산
- 2010.02.03 삼각함수의 합차공식에 대한 증명 2
- 2009.08.10 MIT Strang 교수님의 Linear Algebra 강의
- 2008.09.21 수식 문자모음
- 2008.08.24 시그마 k^2 을 구하는 공식
- 2008.04.13 미적분학의 기초
- 2008.04.13 선형대수의 기초
- 2008.03.07 벡터의 내적 1
점과 직선 사이의 거리 공식: 벡터의 내적을 이용한 유도

참고로 위의 결과를 3차원 공간에 존재하는 평면 ax+by+cz+d=0와 점 (x1,y1,z1)으로 확장해도 마찬가지로 쉽게 점과 평면 사이의 거리를 구할 수 있다. 결과는 다음과 같다. r=|ax1+by1+cz1+d|√a2+b2+c2. n차원 공간에서의 결과는 어떻게 되겠는가?
- b=0인 경우는 점과 직선 사이의 거리는 |m+c/a|이므로 b≠0인 경우를 고려한다. [본문으로]
The Grammar According to West by Douglas B. West

확률변수 K의 확률분포함수가 f_{K}(k)=\binom{n}{k}p^{k}q^{n-k} 로 주어지는 경우 평균과 분산을 구해본다. 평균을 E[K] = \bar{K}라 하면 \bar{K}는 다음과 같다. \bar{K} = \sum_{k=0}^{n}kf_{K}(k). 여기서는 미분을 이용해 이 값을 구해보도록 한다. (x+q)^{n} = \sum_{k=0}^{n}\binom{n}{k}x^{k}q^{n-k} 의 양변을 x에 대해 미분하고 x를 곱하면 \begin{align}nx(x+q)^{n-1} = \sum_{k=0}^{n}k\binom{n}{k}x^{k}q^{n-k} \tag{1} \end{align}이다. 여기서 x = p를 대입하면 p+q = 1이고 (1)의 우변은 \bar{K}이므로 \bar{K} = np이다. 한편 분산은 다음과 관계를 만족함이 알려져 있다. \sigma_{K}^{2} = E[K^{2}]-\bar{K}^{2}.여기서 \bar{K}는 이미 구했으므로 E[K^{2}]를 구하도록 한다. E[K^{2}] = \sum_{k=0}^{n}k^{2}f_{K}(k). 이고 이를 찾기 위해 (1)의 양변을 x에 대해 한 번 더 미분하고 다시 x를 곱하면 다음과 같다. nx(x+q)^{n-1} + n(n-1)x^{2}(x+q)^{n-2} = \sum_{k=0}^{n}k^{2}\binom{n}{k}x^{k}q^{n-k}. 이제 x = p를 대입하면 p+q = 1이므로 이를 정리하면 다음과 같다. E[K^{2}] = \sum_{k=0}^{n}k^{2}\binom{n}{k}p^{k}q^{n-k} = np+n^{2}p^{2}-np^{2}. 따라서 분산은 다음과 같다. \sigma_{K}^{2} = E[K^{2}]-\bar{K}^{2} = (np+n^{2}p^{2}-np^{2})-(np)^{2} = np(1-p) = npq.
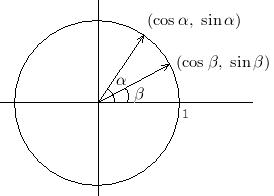
고등학교 3학년이 되어 심화 미적분을 배우면 삼각함수와 관련된 여러 공식들을 배우게 된다. 이들에 대한 자세한 유도는 책에 있지만 벡터의 내적을 이용한 증명이 가장 단순하고 기억하기 쉬운 것 같다.
코사인이나 사인에 관한 합차공식 중 아무거나 하나만 증명하면 나머지 공식들은 이로부터 우글우글 쏟아져 나오므로 맨 처음 시작만을 적겠다.
위와 같이 길이가 1인 두 벡터를 생각하자. 이제 두 벡터의 내적을 구하면
|1||1|\cos(\alpha - \beta) = \cos\alpha \cos\beta + \sin\alpha \sin\beta
이다. \beta 대신에 -\beta를 대입하면 \cos(\alpha+\beta)에 대한 공식을 구할 수 있다. 다시 \beta 대신에 \beta-\pi/2를 대입하면 \sin(\alpha + \beta)에 대한 공식을 얻을 수 있다 (\cos(\theta-\pi/2) = \sin\theta이므로...). 이런 식으로 다른 공식들을 하나씩 증명해 나갈 수 있다.
http://ocw.mit.edu/OcwWeb/Mathematics/18-06Spring-2005/CourseHome/index.htm
예비공식:\begin{align} \sum_{k=1}^{n}k = \frac{n(n+1)}{2}. \tag{1} \end{align}
먼저 \sum_{k=1}^{n}k^2 = 1^2\cdot1 + 2^2\cdot1 + \cdots + n^2\cdot1이고 이는 밑변의 길이가 1이고 높이가 k^2인 직사각형들의 넓이를 모두 합한 것과 같다. 한편, 위의 그림에서 같은 색으로 표시된 영역들에 초점을 두고 생각해 보면 다음과 같은 관계를 얻을 수 있다.\sum_{k=1}^{n}k^2 = (1^2-0^2)n + (2^2-1^2)(n-1) + (3^2-2^2)(n-2) + \cdots + [n^2-(n-1)^2]\cdot1.이를 시그마를 이용해 표현하면 다음과 같다.\sum_{k=1}^{n}k^2 = \sum_{k=1}^{n}[k^2 - (k-1)^2](n-k+1).우변을 전개해서 정리하면 다음과 같은 관계를 얻는다.\begin{align} \sum_{k=1}^{n}k^2 &= \sum_{k=1}^{n}[(2n+3)k - (n+1)] - 2\sum_{k=1}^{n}k^2. \end{align}이제 \sum_{k=1}^{n}k^2을 한쪽으로 묶고 \sum_{k=1}^{n}k항들에 (1)을 대입하여 정리하면 다음을 얻는다.3\sum_{k=1}^{n}k^2 = \frac1{2}n(n+1)(2n+1).그리고 양변을 3으로 나누면 \sum_{k=1}^{n}k^2을 구하는 공식이 된다.
출처 : 밝히리님 블로그
http://blog.daum.net/eigenvalue/10856412
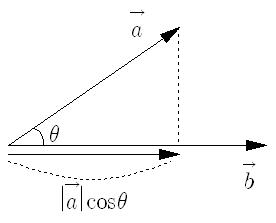
위의 그림에서 보이듯이 한 벡터를 다른 벡터에 정사영 시킨 크기와 다른 벡터의 크기를 곱한 값이 두 벡터의 내적이 된다 (사잇각이 예각일 경우).
문제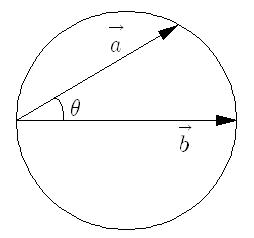 위의 그림과 같이 벡터 \vec{a}와 \vec{b}는 시점이 같고 \vec{a}의 크기는 3이며 \vec{a}의 종점이 원 위에 있다. 벡터 \vec{b}가 원의 중심을 지날때 두 벡터의 내적을 구하시오 답 : 9 |
벡터 \vec{a}를 벡터 \vec{b}에 정사영 시킨 크기가 3이므로 답은 3*3=9 임을 쉽게 알 수 있다.
우리가 쉽게 접하는 일차함수의 그래프 역시 벡터의 내적을 이용해 생각해 볼 수 있다.
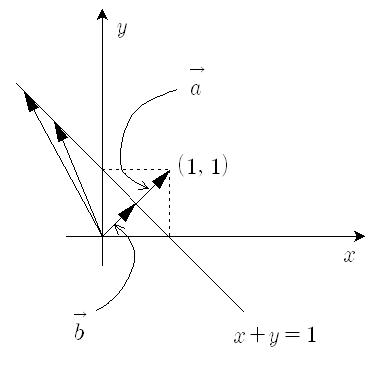
위의 그림에서 x+y=1 의 그래프 위의 모든 벡터들은 벡터 \vec{a}에 정사영 시키면 벡터 \vec{b}와 같은 크기를 같는 벡터가 된다. 즉 (x,y)\boldsymbol{\cdot}(1,1) = 1을 만족하는 모든 벡터들이 직선 x+y=1 위에 그 종점을 두고 있는 것이다. 변수 z를 추가하여 생각하면 x+y+z=1이라는 평면의 방정식 역시 (x,y,z)\boldsymbol{\cdot}(1,1,1) = 1로 놓고 생각해 볼 수 있다.
여기에서 만약 두 벡터가 수직인 경우를 생각해 보자 만약 두 벡터가 수직이라면 한 벡터를 다른 벡터에 정사영시킨 크기는 0이므로 두 벡터의 내적이 항상 0이다. 두 벡터가 수직이라함은 사이각이 90도라는 말이고 따라서 코사인값이 0이므로 내적이 0이다. 이를 이용한 멋진 문제가 또하나 있다.
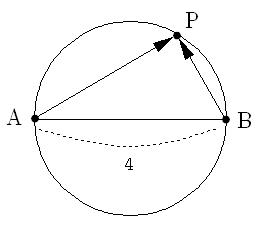
| 문제 평면위에 점 A와 점 B가 있다. 두 점 사이의 거리가 4라고 하자. 평면위에 임의의 점 P가 존재하여 벡터 \vec{AP}와 벡터 \vec{BP}의 내적이 항상 0이라고 할 때 점 P가 그리는 자취의 길이는? 답 : 4\pi |
문제의 조건에 맞게 그림을 그려 보면 점 P는 아래 그림처럼 원 위를 움직이는 점임을 알 수 있다. 따라서 점 P의 자취는 지름이 4인 원의 둘레길이가 되고 따라서 답이 4\pi이다.
 Prev
Prev




 invalid-file
invalid-file