두 벡터 \(\vec{a},\vec{b}\)의 내적은 두 벡터 기호 사이에 점을 찍어 \(\vec{a}\boldsymbol{\cdot}\vec{b}\) 표현하고 \(a\) 내적 \(b\)라고 읽는다. 고등학교 수학에서 벡터의 내적은 다음과 같이 정의한다.
\begin{align*}
\vec{a}\boldsymbol{\cdot}\vec{b} = |\vec{a}||\vec{b}| \cos\theta.
\end{align*}
그 의미를 다시 생각해 보면
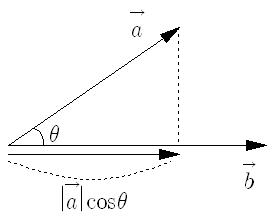
위의 그림에서 보이듯이 한 벡터를 다른 벡터에 정사영 시킨 크기와 다른 벡터의 크기를 곱한 값이 두 벡터의 내적이 된다 (사잇각이 예각일 경우).
벡터 \(\vec{a}\)를 벡터 \(\vec{b}\)에 정사영 시킨 크기가 3이므로 답은 3*3=9 임을 쉽게 알 수 있다.
우리가 쉽게 접하는 일차함수의 그래프 역시 벡터의 내적을 이용해 생각해 볼 수 있다.
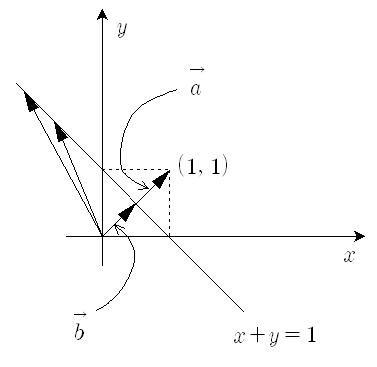
위의 그림에서 \(x+y=1\) 의 그래프 위의 모든 벡터들은 벡터 \(\vec{a}\)에 정사영 시키면 벡터 \(\vec{b}\)와 같은 크기를 같는 벡터가 된다. 즉 \((x,y)\boldsymbol{\cdot}(1,1) = 1\)을 만족하는 모든 벡터들이 직선 \(x+y=1\) 위에 그 종점을 두고 있는 것이다. 변수 \(z\)를 추가하여 생각하면 \(x+y+z=1\)이라는 평면의 방정식 역시 \((x,y,z)\boldsymbol{\cdot}(1,1,1) = 1\)로 놓고 생각해 볼 수 있다.
여기에서 만약 두 벡터가 수직인 경우를 생각해 보자 만약 두 벡터가 수직이라면 한 벡터를 다른 벡터에 정사영시킨 크기는 0이므로 두 벡터의 내적이 항상 0이다. 두 벡터가 수직이라함은 사이각이 90도라는 말이고 따라서 코사인값이 0이므로 내적이 0이다. 이를 이용한 멋진 문제가 또하나 있다.
위의 그림에서 보이듯이 한 벡터를 다른 벡터에 정사영 시킨 크기와 다른 벡터의 크기를 곱한 값이 두 벡터의 내적이 된다 (사잇각이 예각일 경우).
문제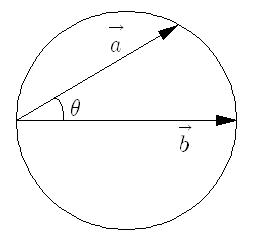 위의 그림과 같이 벡터 \(\vec{a}\)와 \(\vec{b}\)는 시점이 같고 \(\vec{a}\)의 크기는 3이며 \(\vec{a}\)의 종점이 원 위에 있다. 벡터 \(\vec{b}\)가 원의 중심을 지날때 두 벡터의 내적을 구하시오 답 : 9 |
벡터 \(\vec{a}\)를 벡터 \(\vec{b}\)에 정사영 시킨 크기가 3이므로 답은 3*3=9 임을 쉽게 알 수 있다.
우리가 쉽게 접하는 일차함수의 그래프 역시 벡터의 내적을 이용해 생각해 볼 수 있다.
위의 그림에서 \(x+y=1\) 의 그래프 위의 모든 벡터들은 벡터 \(\vec{a}\)에 정사영 시키면 벡터 \(\vec{b}\)와 같은 크기를 같는 벡터가 된다. 즉 \((x,y)\boldsymbol{\cdot}(1,1) = 1\)을 만족하는 모든 벡터들이 직선 \(x+y=1\) 위에 그 종점을 두고 있는 것이다. 변수 \(z\)를 추가하여 생각하면 \(x+y+z=1\)이라는 평면의 방정식 역시 \((x,y,z)\boldsymbol{\cdot}(1,1,1) = 1\)로 놓고 생각해 볼 수 있다.
여기에서 만약 두 벡터가 수직인 경우를 생각해 보자 만약 두 벡터가 수직이라면 한 벡터를 다른 벡터에 정사영시킨 크기는 0이므로 두 벡터의 내적이 항상 0이다. 두 벡터가 수직이라함은 사이각이 90도라는 말이고 따라서 코사인값이 0이므로 내적이 0이다. 이를 이용한 멋진 문제가 또하나 있다.
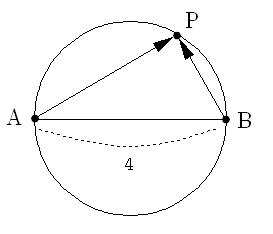
| 문제 평면위에 점 \(A\)와 점 \(B\)가 있다. 두 점 사이의 거리가 4라고 하자. 평면위에 임의의 점 \(P\)가 존재하여 벡터 \(\vec{AP}\)와 벡터 \(\vec{BP}\)의 내적이 항상 0이라고 할 때 점 \(P\)가 그리는 자취의 길이는? 답 : \(4\pi\) |
문제의 조건에 맞게 그림을 그려 보면 점 \(P\)는 아래 그림처럼 원 위를 움직이는 점임을 알 수 있다. 따라서 점 \(P\)의 자취는 지름이 4인 원의 둘레길이가 되고 따라서 답이 \(4\pi\)이다.
